速水グループ

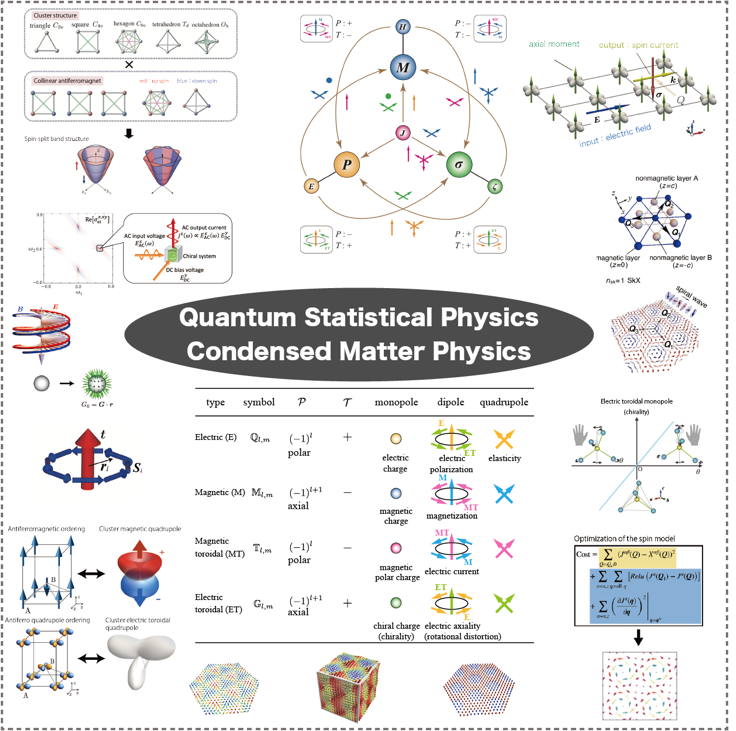
物質科学の魅力の1つは、組み合わせる元素の種類や組成比、結晶構造の違いによって、磁性や超伝導、誘電性などの異なる物性が現れる多様性です。その中でも強相関電子系では、固体中の電子同士が互いのクーロン反発力の影響を強く受けることにより、電荷の自由度だけではなく、スピンや軌道の自由度といった他の内部自由度が重要な役割を果たすようになります。これらの内部自由度は、スピン軌道相互作用や結晶構造の歪みといった様々な要素を通じて絡み合うことによって、通常の金属や半導体では考えられない面白い性質を生み出します。
我々の研究室では、こうした強相関電子系が示す多彩で魅力的な物性現象を理解するうえで重要な要素を最小限だけ取り入れたモデルに対して、量子統計力学に基づいた理論解析と数値シミュレーションを相補的に用いた研究を行っています。研究を通して、これまでにない新しい量子状態や物性現象の発見・理解といった基礎物理の開拓に留まらず、次世代のテクノロジーの理論的な基盤を提供することを目指しています。
興味をもっている最近の研究テーマとしては以下のものがあります。

• ミクロな多極子に基づいた電子物性表現論の構築
• 電気・磁気・弾性・熱・光自由度間にまたがる新しいマルチフェロイクス概念の提案
• 新奇電子秩序相、超伝導相の機構解明と理解
• トポロジーと磁性の絡み合いにより創出されるトポロジカルスピン秩序：スキルミオン・ヘッジホッグ・メロン
• 反強磁性スピントロニクスの実現に向けた機能物性開拓
• 機械学習を用いた効率的物性探索
• 第一原理バンド計算を用いた現実物性の定量的解析
• 実験で観測される非自明な電子相および物性現象の機構解明

研究室ウェブサイト（速水グループ）

奥田グループ

スピングラスとフラストレート系

規則正しく並んだイジングスピン(↑と↓しか向きが取れないスピン)の集まりを考えたとき、隣のスピンを同じ向きに揃えようとする相互作用が働いてる場合、ある温度以下では多くのスピンは同じ向きに揃ってしまいます。隣のスピンを逆向きに揃えようとする相互作用が働いてる場合、ある温度以下ではスピンは↑↓↑↓・・・上向きと下向きを交互に取るようなスピン配位になります。どちらの場合も高温では熱ゆらぎの効果が支配的でスピンは一つのスピン配位に落ち着くことができません。さて、同じ向きに揃えようとする相互作用と逆向きに揃えようとする相互作用がごちゃまぜにある場合、スピンはどのような振る舞いを見せるでしょうか？

非線形動力学、特に、結合振動子系についての研究

ここでいう振動子はエネルギーの注入と散逸のバランスのもとに現れる非線形振動子で、物理系のみならず化学反応系や生物の体内時計、神経回路網など自然界に広く存在している。このような振動子は一般に他の振動子と相互作用しており、その結果として、集団同期やカオスなど複雑な現象が現れる。これらの現象を理解するために、簡単な数理モデルの解析や数値実験などの方法を用いた理論的研究を行っている。

複雑ネットワーク上の相転移現象

複雑ネットワークとは

私達が住むこの世界には、WWW(World Wide Web)や友人関係、食物連鎖など様々なネットワークが存在しています。これらのネットワークの構造は、従来の物理学で扱われてきた格子のような均一構造ではないことは明らかです。近年、このような複雑なネットワークの構造に対する関心が高まっています。現実の複雑なネットワークには、スケールフリー性・クラスター性・スモールワールド性などの、いくつかの共通した性質があることが分かってきています。私達の目的の1つは、これらの性質を再現するような数学的なモデルを作成することです。ネットワークへの数学的アプローチは、数学の分野ではグラフ理論により古くからなされていました。最近では、WWWなどの大規模なデータ収集が可能なネットワークの出現が、モデル作成の大きな助けになっています。さらに、もう一つの目的は、モデル化したネットワーク上で起きる様々なダイナミクスについて調べることです。ランダムウォークや、パーコレーション（浸透現象）、Spin Systemなど、従来物理の分野で研究されてきた現象が、ネットワーク上では従来とは異なった振る舞いを見せることが指摘されています。私達は、統計力学の手法を生かし、様々なダイナミクスについて解析を進めています。

複雑ネットワーク上の相転移現象

磁性体のスピンモデルやパーコレーション理論などの相転移を伴う現象を考える時、一般には2次元正方格子や3次元立方格子などの、各頂点が規則的に並んだいわゆる”格子”を思い浮かべますが、各頂点が不均一な繋がりをした”ネットワーク”で転移を伴う現象を考えることもできます。ある種の構造を持ったネットワークでは、格子系の、無秩序相から転移点を境に秩序相へと相転移するシナリオではなく、無秩序相と秩序相の間に中間的な相（臨界相）が現れるような転移を起こす事が知られています。しかし、その臨界相での振る舞いについてはあまり研究がされていません。そこで、臨界相の現れるネットワークで、かつ厳密解を解析的に求めることの出来るモデルとして階層格子上のパーコレーションを考え、臨界相での系の振る舞いを調べています。

研究室ウェブサイト（旧 物性理論I研究室）